Cube Surface Puzzle

Given a set of six pieces, “Cube Surface Puzzle” is to construct a hollow cube with filled surface. Pieces of a puzzle is made of a number of small unit cubes laid grid-aligned on a plane. For a puzzle constructing a cube of its side length n, unit cubes are on either of the following two areas.

• Core (blue): A square area with its side length n−2. Unit cubes fill up this area.
• Fringe (red): The area of width 1 unit forming the outer fringe of the core. Each unit square in this area may be empty or with a unit cube on it.

Each piece is connected with faces of its unit cubes. Pieces can be arbitrarily rotated and either side of the pieces can be inside or outside of the constructed cube. The unit cubes on the core area should come in the centers of the faces of the constructed cube.

Consider that we have six pieces in Fig. E-1 (The first dataset of Sample Input). Then, we can construct a cube as shown in Fig. E-2.

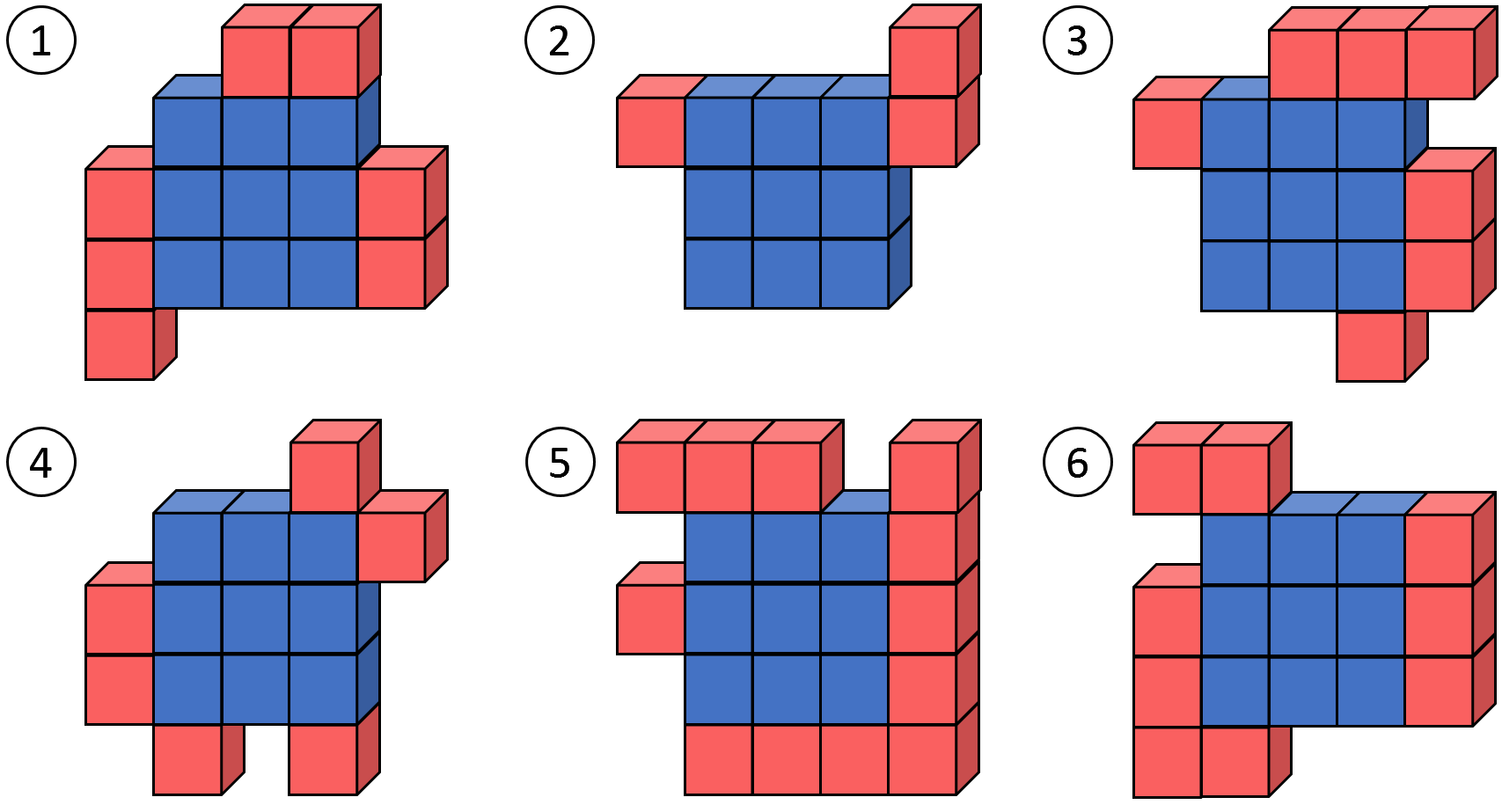
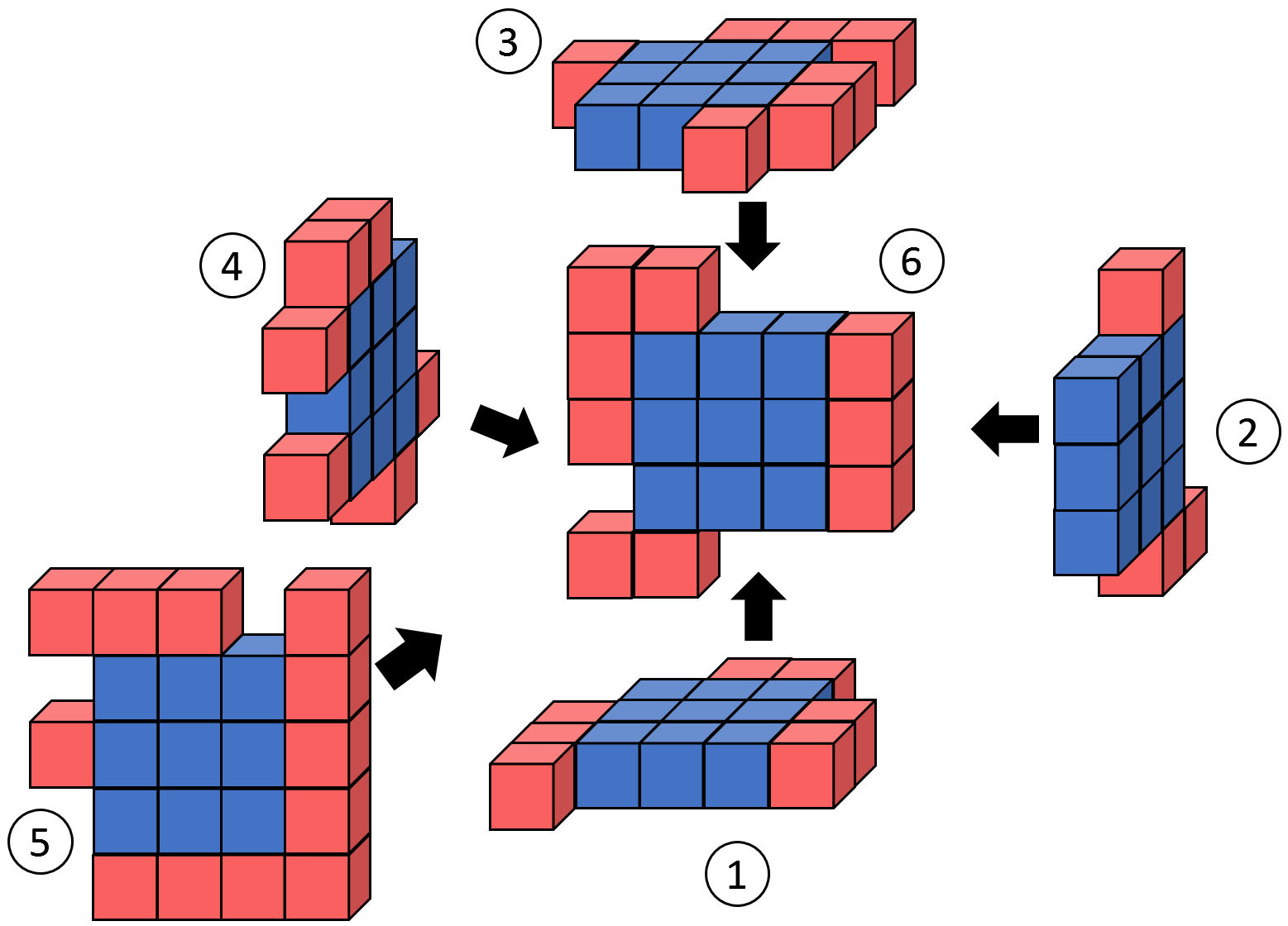
Mr. Hadrian Hex has collected a number of cube surface puzzles. One day, those pieces were mixed together and he cannot find yet from which six pieces he can construct a cube. Your task is to write a program to help Mr. Hex, which judges whether we can construct a cube for a given set of pieces.

Input

The input consists of at most 200 datasets, each in the following format.

n
x_1,1x_1,2 … x_1,n
x_2,1x_2,2 … x_2,n
…
x_6n,1x_6n,2 … x_6n,n

The first line contains an integer n denoting the length of one side of the cube to be constructed (3 ≤ n ≤ 9, n is odd). The following 6n lines give the six pieces. Each piece is described in n lines. Each of the lines corresponds to one grid row and each of the characters in the line, either ‘X’ or ‘.’, indicates whether or not a unit cube is on the corresponding unit square: ‘X’ means a unit cube is on the column and ‘.’ means none is there.

The core area of each piece is centered in the data for the piece.

The end of the input is indicated by a line containing a zero.

Output

For each dataset, output “Yes” if we can construct a cube, or “No” if we cannot.

Sample Input

5
..XX.
.XXX.
XXXXX
XXXXX
X....
....X
XXXXX
.XXX.
.XXX.
.....
..XXX
XXXX.
.XXXX
.XXXX
...X.
...X.
.XXXX
XXXX.
XXXX.
.X.X.
XXX.X
.XXXX
XXXXX
.XXXX
.XXXX
XX...
.XXXX
XXXXX
XXXXX
XX...
5
..XX.
.XXX.
XXXXX
XXXX.
X....
....X
XXXXX
.XXX.
.XXX.
.....
.XXXX
XXXX.
.XXXX
.XXXX
...X.
...X.
.XXXX
XXXX.
XXXX.
.X.X.
XXX.X
.XXXX
XXXXX
.XXXX
.XXXX
XX...
XXXXX
XXXXX
.XXXX
XX...
0

Output for the Sample Input

Yes
No

---