Presentation

You are a researcher investigating algorithms on binary trees. Binary tree is a data structure composed of branch nodes and leaf nodes. Every branch nodes have left child and right child, and each child is either a branch node or a leaf node. The root of a binary tree is the branch node which has no parent.

You are preparing for your presentation and you have to make a figure of binary trees using a software. You have already made a figure corresponding to a binary tree which is composed of one branch node and two leaf nodes (Figure 1.) However, suddenly the function of your software to create a figure was broken. You are very upset because in five hours you have to make the presentation in front of large audience.

You decided to make the figure of the binary trees using only copy function, shrink function and paste function of the presentation tool. That is, you can do only following two types of operations.

• Copy the current figure to the clipboard.

  • The figure copied to the clipboard before is removed.

• Paste the copied figure (with shrinking, if needed), putting the root of the pasted figure on a leaf node of the current figure.

  • You can paste the copied figure multiple times.

Moreover, you decided to make the figure using the minimum number of paste operations because paste operation is very time cosuming. Now, your job is to calculate the minimum possible number of paste operations to produce the target figure.

Figure 1: initial state

For example, the answer for the instance of sample 1(Figure 4) is 3, because you can produce the target figure by following operations and this is minimum.

Figure 2: intermediate 1

Figure 3: intermediate 2

Figure 4: Goal

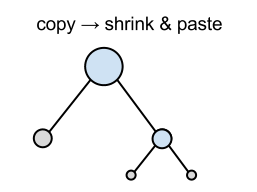
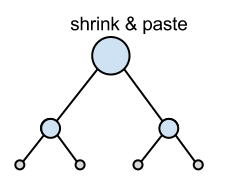
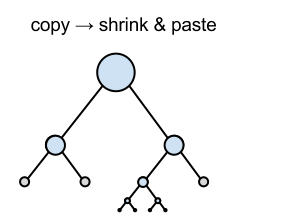
Input

The input is a line which indicates a binary tree. The grammar of the expression is given by the following BNF.

<tree> ::= <leaf> | "(" <tree> <tree> ")"
<leaf> ::= "()"

Every input obeys this syntax. You can assume that every tree in the input has at least 1 branch node, and that it has no more than 10^5 branch nodes.

Output

A line containing the minimum possible number of paste operations to make the given binary tree.

Sample Input 1

((()())(((()())(()()))()))

Output for the Sample Input 1

3

Sample Input 2

(((()())(()()))(()()))

Output for the Sample Input 2

4

Sample Input 3

((()(()()))((()(()()))()))

Output for the Sample Input 3

3

Sample Input 4

(()())

Output for the Sample Input 4

0

---