ヘリリンは二次元平面上における長さ2Lの線分の形状をしている。
ヘリリンのまわりには、線分の形状をしたいくつかの障害物が存在している。

ヘリリンは障害物に接すると体力が削られてしまう。
完璧主義のヘリリンは無傷でゴールすることにした。

ヘリリンは以下の行動ができる。

• 平行移動
• ヘリリンを表す線分の中点を中心として、反時計周りにちょうど 180 / r 度だけ回転する

ただし、二次元平面は上方向にy軸をとる。

ヘリリンのまわりに、2 点 S, G がある。
始めはヘリリンの中心は点 S にあって、x軸に平行な状態になっている。

ヘリリンは、平行移動するのは得意だが、回転するのは不得意である。
あなたの仕事は、ヘリリンが中心を点 S から点 G まで移動させるまでに必要な、最小の回転行動の回数を求めることである。
移動させることができない場合は、そのことも検出せよ。

ただし、以下のことに注意せよ。

• ヘリリンは移動しながら回転することはできない。
• ヘリリンが回転する途中で障害物にぶつかりうる場合は、回転することはできない。
• 障害物が互いに交差していることはあり得る。
• 線分は十分小さい有限の太さを持つものとして扱う。最後のサンプルを見よ。

Input

入力は以下の形式で与えられる。

L r
sx sy
gx gy
n
x11 y11 x12 y12
...
xn1 yn1 xn2 yn2

Lはヘリリンの半分の長さを表す。 rは回転角度を定めるものである。 (s_x, s_y)は点 S、(g_x, g_y)は点 G の座標である。 nは障害物の数を表す。 (x_i1, y_i1)と(x_i2, y_i2)はi番目の障害物を表す線分の端点である。

Constraints

入力は以下の制約を満たす。

• 1 ≤ n ≤ 30
• 2≤ r ≤ 11
• 1 ≤ L ≤ 10⁵
• 入力に含まれる座標の各成分は絶対値が10⁵以下
• 入力に含まれる数値はすべて整数
• i = 1, . . . , nについて (x_i1, y_i1) ≠ (x_i2, y_i2)
• ヘリリンをスタート地点にx軸に水平な状態で配置したとき、障害物との（線分と線分との）距離は 10⁻³ より大きい
• 障害物を表す線分の端点を、両方向に 10⁻³ だけ延ばしても縮めても解は変わらない
• Lを 10⁻³ だけ増減させても解は変わらない
• 障害物の線分をl_iと書くことにすると、1 ≤ i ≤ j ≤ nであって、l_iとl_jの距離が2L以下であるような組(i, j)は高々100個
• ゴール地点は障害物に乗っていることはない

Output

スタート地点からゴール地点まで移動するために必要な最小の回転行動の回数を1行に出力せよ。 移動させることができない場合は、-1を1行に出力せよ。

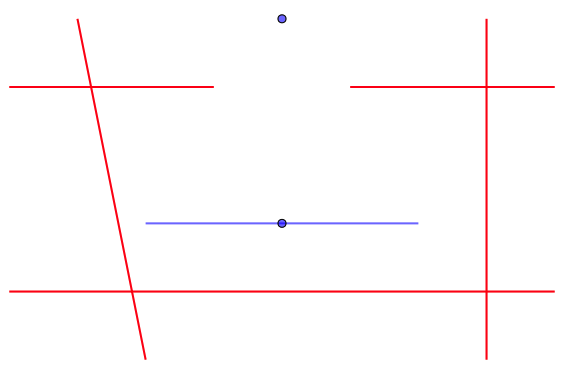
Sample Input 1

1 2
3 3
2 -1
4
1 0 1 5
0 1 4 1
0 4 6 4
5 0 5 5

Output for the Sample Input 1

1

• ヘリリンを90度回転させることで、隙間を抜けることができる。

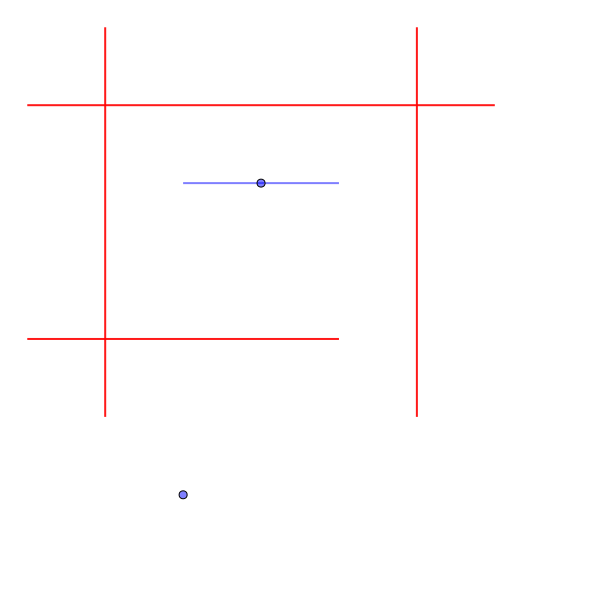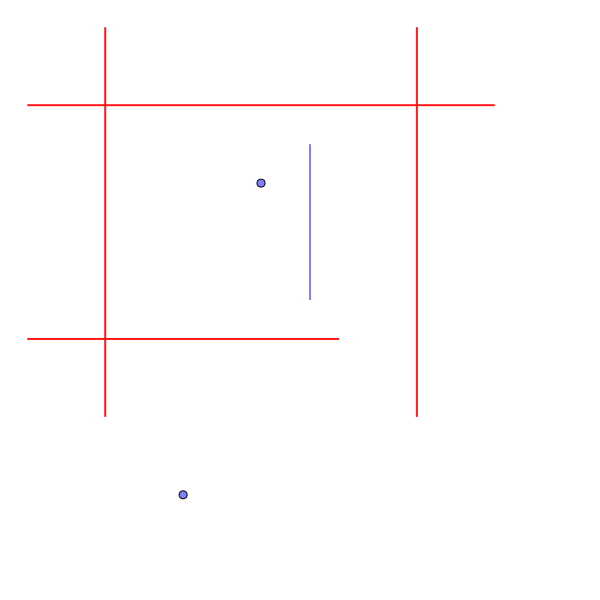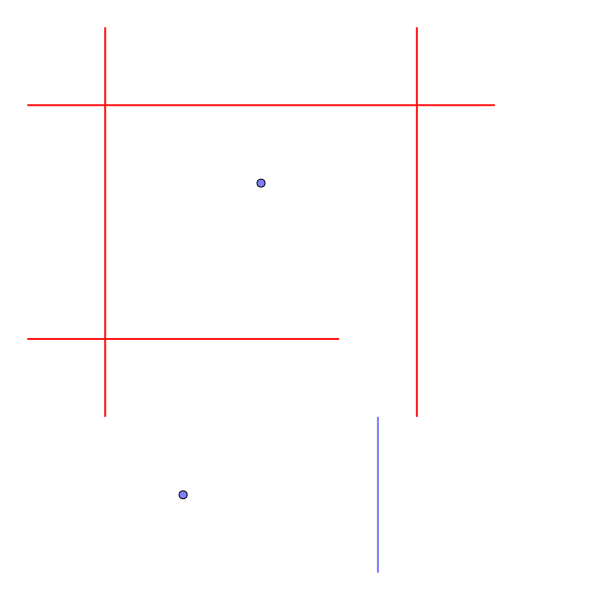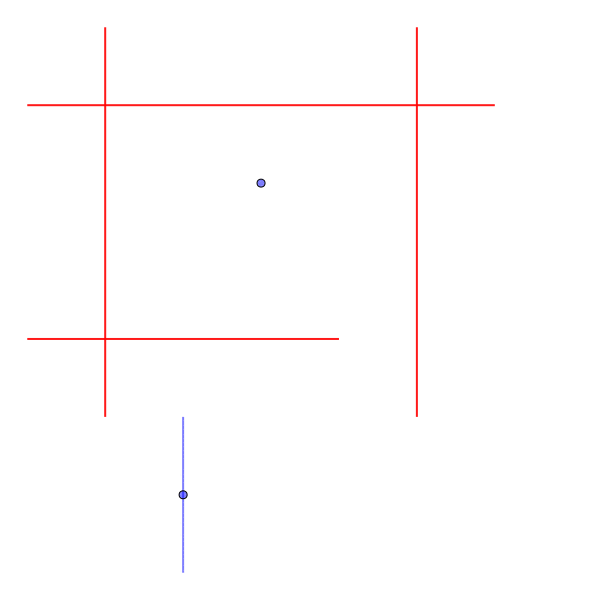
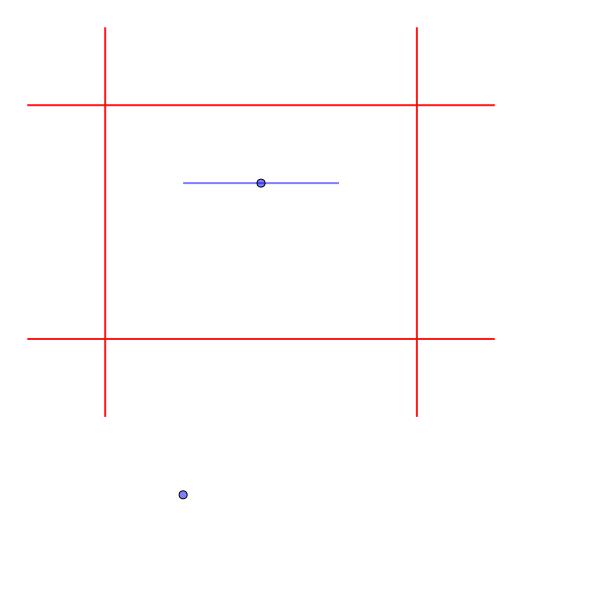
Sample Input 2

1 2
3 3
2 -1
4
1 0 1 5
0 1 6 1
0 4 6 4
5 0 5 5

Output for the Sample Input 2

-1

• ヘリリンは完全に囲まれているので、ゴールまで移動することができない。

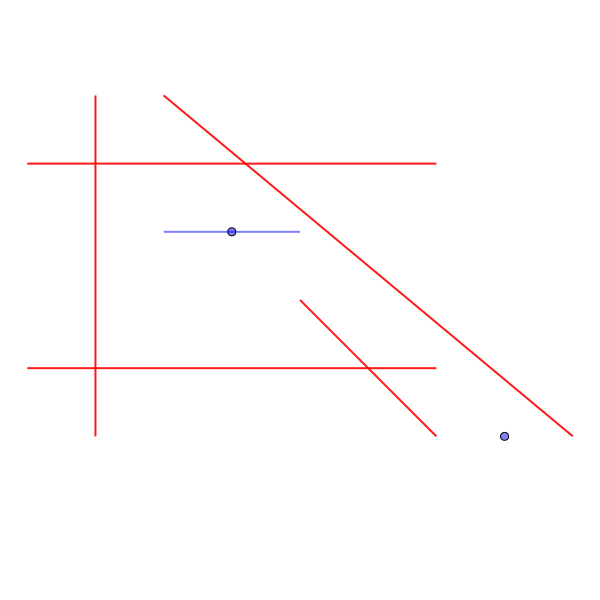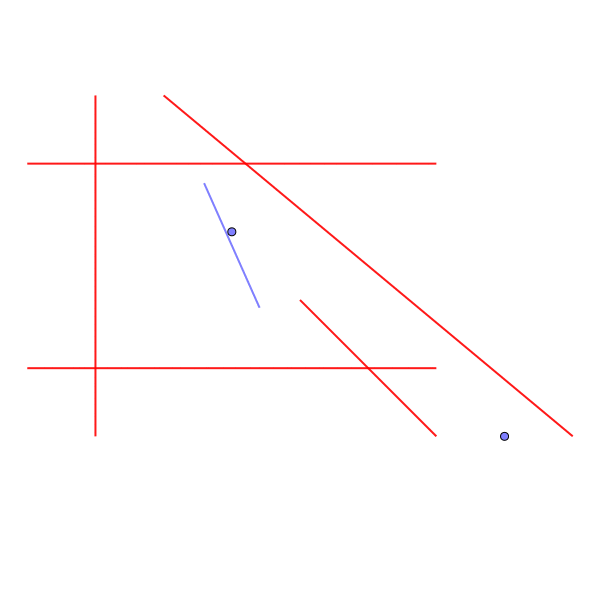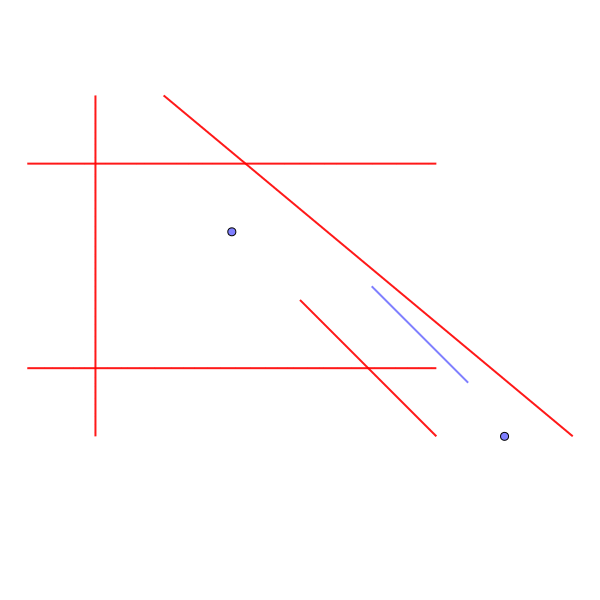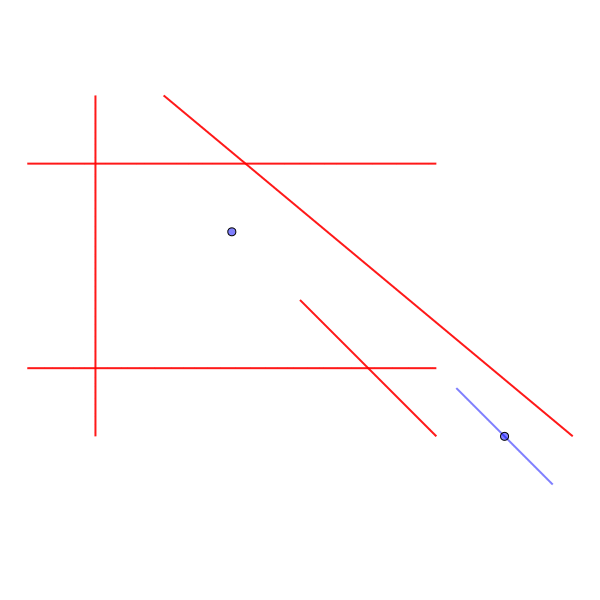
Sample Input 3

1 4
3 3
7 0
5
1 0 1 5
0 1 6 1
0 4 6 4
8 0 2 5
6 0 4 2

Output for the Sample Input 3

3

• 斜めの経路を通るためには、3回反時計周りに回転しなければならない。

Sample Input 4

2 2
4 2
4 5
5
1 5 2 0
0 4 3 4
0 1 8 1
7 0 7 5
8 4 5 4

Output for the Sample Input 4

-1

• ヘリリンは障害物にぴったり接することができないので、隙間のところで回転してゴールまで移動することはできない。

---