Dice Stamp

サイコロスタンプ

あなたは地元の縁日で，今までに見たことがないゲームの出店を発見した． N 個の6面サイコロを，ボード上に落として転がすゲームだ． より正確には， N 個のボタンが N 個のサイコロに1対1に紐付いており，ボタンを押すことで対応したサイコロがボードに落ちる． ボタンを好きなように N 回押し，サイコロを N 回落として転がすことで得点を得るゲームである．

ゲームのより詳細なルールを説明しよう． ゲームで使用する N 個のサイコロはすべて各辺の長さが1の立方体であり，ボードは長さが1の正方形のマスに区切られた十分に広い平面である． ゲーム開始前，ボードの各マスにはすべて0が書かれている． 各サイコロの各面には整数が書かれている．これは1から6までとは限らないし，サイコロごとに違う数が書かれていることもある．

ゲームで用いる筐体には N 個のボタンが付いており， N 個のサイコロと1対1に紐付いている． いずれかのボタンを押すと，対応したサイコロが機械から排出されてボードに落ち，何度か回転する． 回転の途中，サイコロの下面は必ずボードのいずれかのマスにぴったりと重なる． 下面がマスに触れる度，そのマスに書かれていた数が，サイコロの下面に書かれた数で上書きされる． これは落下により初めてボードに触れたときも含む． 回転が止まった後，サイコロはボードから取り除かれ，元の排出装置へと戻される． ボタンを N 回押した後，ボードに書かれた数の和が最終得点となる． 同じボタンを複数回押すことはできるが，1つ前に排出したサイコロの回転が終わり，排出装置に戻るまで次のボタンを押すことはできない．

さて，出店のおっちゃんはサイコロの排出の仕方はランダムだと主張しているが，注意深いあなたは，他の客が遊ぶ様子を観察することで，同じボタンを押した時の挙動がそれまでのボタンの押し方に依らず完全に同一であることに気付いた． より具体的には， i 番目のボタンを押したときの挙動は以下のように決定的である．

1. i 番目のサイコロが排出される．
2. このサイコロは内部で決められたマスに決められた向きで落下する．この向きは必ず，マスの正方形と下面の正方形とがぴったりと重なる向きである．
3. サイコロは前後左右4方向いずれかに回転することを繰り返す．回転回数やそれぞれの回転の方向も，内部で決められている．
4. 決められた回転が終了すると，サイコロはボードから取り除かれ，排出装置に戻される．

ここで，便宜上3次元空間を考え，マスの辺に平行な向きにそれぞれ x 軸と y 軸をとり，サイコロ上面が向く方向を z 軸正方向とする. この時，サイコロの回転は x, y 軸の正，負方向の4通りであり，それぞれ下図のようになる．ただし，図中の記号は後述の入力形式に対応している．

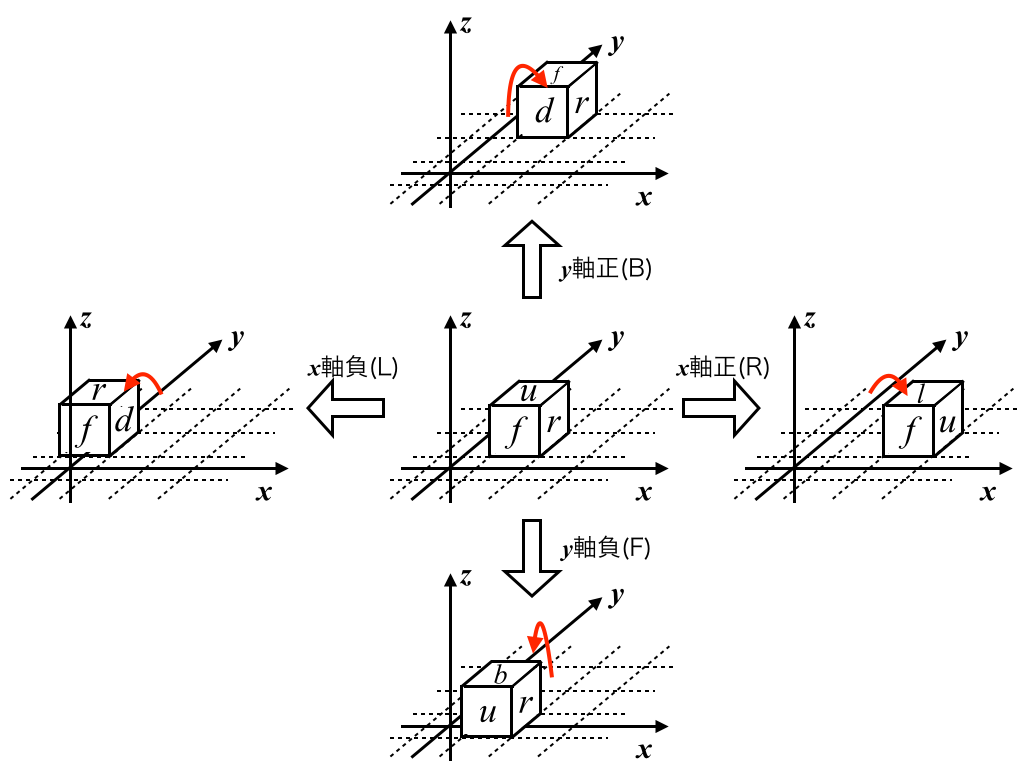
決定的に動くとはなんて詐欺だ，と憤りを感じたものの，あなたは N 回のボタンの押し方によって最終得点を変えられることに気が付いた．

あなたは入念な観察により各サイコロの各面に書かれた数や落とされる初期位置・向き・その後の回転の仕方に至るまで完全な情報を揃えた． 集めた情報に基づいて，最善のボタンの押し方で得られるこのゲームの最高得点を求めよ．

Input

入力は40個以下のデータセットからなる．各データセットは以下の形式で表される．

N
1番目のサイコロの情報
...
N 番目のサイコロの情報

入力の最初の行は，サイコロの個数を表す1つの整数 N からなる．1 ≤ N ≤ 15 と仮定してよい． 以降， N 個のサイコロの情報が続く．

それぞれのサイコロの情報は，以下の形式で表される．

x y
l r f b d u
rot

1行目は2つの整数 x, y からなり，排出されたときにサイコロが落とされるマスの中心の座標 (x, y) を表す．-1,000 ≤ x, y ≤ 1,000 と仮定してよい．

2行目は6つの整数 l, r, f, b, d, u からなり，各面に書かれた数を表す． l, r, f, b, d, u はそれぞれ，落とされたときに x 軸負方向， x 軸正方向， y 軸負方向， y 軸正方向， z 軸負方向， z 軸正方向を向いている面に書かれた数である．1 ≤ l, r, f, b, d, u ≤ 100 と仮定してよい．

3行目は回転の仕方を表す文字列 rot からなる． rot は 'L', 'R', 'F', 'B' のみからなる文字列であり，1文字以上，30文字以下である． rot の j 番目の文字は j 回目の回転の方向を表しており，文字が 'L', 'R', 'F', 'B' のときそれぞれ， x 軸負方向，x 軸正方向，y 軸負方向，y 軸正方向に回転することを示す．

入力の終わりは，1つのゼロを含む1行で示される．

Output

各データセットについて， N 回のボタンの押し方を工夫することで得られる最高得点を1行で出力せよ． 各出力行はこの数値以外の文字を含んではならない．

Sample Input

1
0 0
1 2 3 4 5 6
RRRRBBBBLLLLFFFF
2
0 0
1 1 1 1 1 1
RRR
2 2
100 100 100 100 100 100
FFF
1
1000 -1000
1 2 3 4 5 6
LFRB
4
-3 -4
1 2 3 4 5 6
BBBBBBBB
4 -3
11 12 13 14 15 16
LLLLLLLL
3 4
21 22 23 24 25 26
FFFFFFFF
-4 3
31 32 33 34 35 36
RRRRRRRR
3
-2 -2
9 3 1 1 1 1
RRRRBLLLBRRBLB
0 -3
2 5 2 5 2 1
BBLBBRBB
3 0
10 7 2 10 1 5
LLFLLBLL
0

Output for Sample Input

64
403
10
647
96

---