H - Bit Operation Game

N 頂点の根付き木が与えられる。 頂点には 0 から N − 1 の番号がついており、0番目の頂点が根を表す。 根には T = 0 が、それ以外の頂点には

• T=T&X
• T=T&Y
• T=T|X
• T=T|Y
• T=T^X
• T=T^Y

のいずれかの操作が書かれている。 ここでの演算子 &, |, ^ はそれぞれビット演算子 and, or, xor, を意味する。

A君とB君はこの木を使って以下のゲームを M 回行った。 二人は根からスタートし、子頂点を選び進むという操作を、A君から始め葉に到達するまで交互に行う。 通ったノードに書かれている操作を、通った順に適用した時の、最終的な T の値がスコアになる。 B君はできるだけスコアを小さくしたいと考えており、またA君は大きくしたいと考えている。 M回のゲームの X, Y の値が与えられるので、二人が最適な選択をした時の各ゲームのスコアを出力せよ。

Constraints

• 1 ≤ N ≤ 100000
• 1 ≤ M ≤ 100000
• 0 ≤ X, Y < 2^{16}

Input Format

入力は以下の形式で標準入力から与えられる。

N M
o_1
o_2
...
o_{N−1}
u_1 v_1
u_2 v_2
...
u_{N−1} v_{N−1}
X_1 Y_1
X_2 Y_2
...
X_M Y_M

1 行目には木の頂点数 N と、行われるゲーム数を表す整数 M が入力される。
2 行目から N 行目にかけて、1 ... N−1 番目の頂点に書かれている操作が入力される。
さらに続けて N−1 行に、各辺により繋がれる 2 頂点の番号が入力される。
最後に M 回のゲームにおける X, Y の値が M 行に渡り入力される。

Output Format

各ゲームでの最終的な T の値をそれぞれ M 行に出力せよ。

Sample Input 1

6 3
T=T|X
T=T|Y
T=T|Y
T=T^Y
T=T&X
0 1
0 2
1 3
1 4
2 5
5 6
3 5
0 0

Sample Output 1

4
6
0

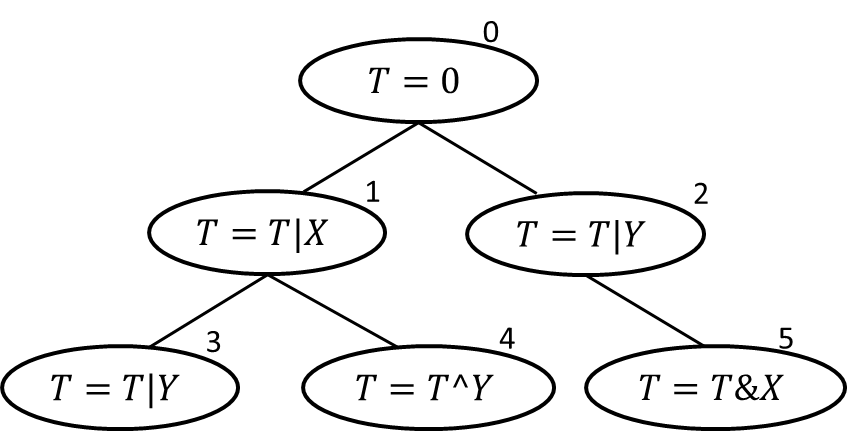
X = 5, Y = 6 の場合、頂点 0 -> 2 -> 5 と進み、T = 5 & 6 = 4 になります
X = 3, Y = 5 の場合、頂点 0 -> 1 -> 4 と進み、T = 3 ^ 5 = 6 になります
X = 0, Y = 0 の場合、どこを通っても T は 0 から変化しません

---