D: 水槽
問題
AORイカちゃんは縦 $1$ 横 $N$ の大きさの水槽をもらった。水槽は水を入れるのに十分な高さがある。 水槽には $N-1$ 個の仕切りがあり $N$ 個の区画に等間隔に区切られている。 ここに水を注いだところ、各区画の水の高さは $a_i$ になった。
AORイカちゃんはいくつか仕切りを取り除き、区画の数を $M$ 個以下にすることにした。 仕切りを取り除き終わった時、各区画の水の高さの総和の最大値を求めよ。
なお、仕切りの厚さは無視できるものとする。
制約
- $1 \le N \le 500$
- $1 \le M \le N$
- $1 \le a_i \le 10^9$
- 入力は全て整数
入力
$N \ M$
$a_1 \cdots a_N$
出力
各区画の水の高さの総和の最大値を一行で出力せよ。また末尾に改行を出力せよ。 相対誤差または絶対誤差が $10^{-6}$ 以下であれば許容される。
サンプル
サンプル入力 1
5 3 9 1 2 3 9
サンプル出力 1
20.000000
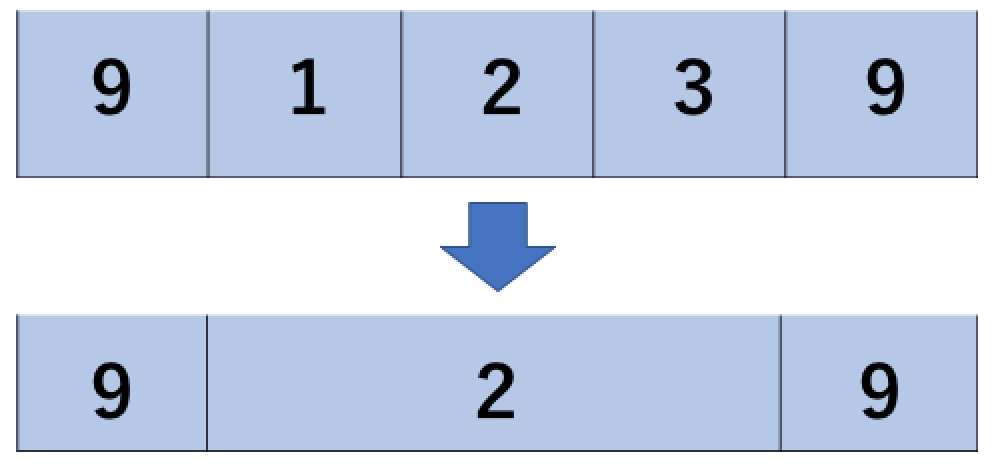
$a_2$ と $a_3$ 、$a_3$ と $a_4$ の間の仕切りをとると、その区画の水の高さは $\frac{(1 + 2 + 3)}{3} = 2$ となる。 各区画の水の高さは $9 \ 2 \ 9$ となりこれが最大である。
サンプル入力 2
4 1 14 4 9 7
サンプル出力 2
8.500000
サンプル入力 3
8 3 11 18 9 20 4 18 12 14
サンプル出力 3
44.666667