L - Flipping a Path
問題文
$N$ 頂点 $M$ 辺の単純有向グラフが与えられます。
このグラフの頂点には $1$ から $N$ までの番号がついていて、辺には $1$ から $M$ までの番号がついています。
辺 $i$ $(1 \le i \le M)$ は、頂点 $u_i$ から頂点 $v_i$ へ向かう辺です。
次の条件を満たす辺素パスが存在するか判定し、存在する場合はそのようなパスの長さの最小値を求めてください。
- パスに含まれるすべての辺の向きを逆にすると、グラフ全体が強連結になる。
ここで長さ $K$ $(K \ge 0)$ の辺素パスとは、次の条件を満たす辺の番号の列 $(e_1, e_2, \ldots, e_K)$ のことです。
- $1 \le i \le K-1$ について $v_{e_i} = u_{e_{i+1}}$ である。
- どのような $1 \le i < j \le K$ についても、$e_i \ne e_j$ である。
特にこの問題では、長さ $K$ が $0$ となるものも辺素パスとして認めることにします。
また、「グラフが強連結である」とは、「そのグラフのどのような $2$ 頂点 $s, t$ $(s \ne t)$ についても、$s$ から $t$ への辺素パス、つまり、$u_{e_0} = s$ かつ $v_{e_K} = t$ を満たす辺素パスが存在する」ということです。
入力
入力は以下の形式で標準入力から与えられる。
$N$ $M$ $u_1$ $v_1$ $u_2$ $v_2$ $\vdots$ $u_M$ $v_M$
制約
- $2 \le N \le 10^5$
- $1 \le M \le \min (10^5, N(N-1))$
- $1 \le u_i \le N$
- $1 \le v_i \le N$
- $u_i \ne v_i$
- どのような $(i, j)$ $(1 \le i < j \le M)$ についても、$(u_i, v_i) \ne (u_j, v_j)$
出力
条件を満たす辺素パスが存在しない場合は -1 を出力せよ。
そうでない場合は、条件を満たすパスの長さの最小値を出力せよ。
入力例 1
4 5
1 2
1 3
2 3
2 4
3 4
出力例 1
2
与えられるグラフは次のようになります。
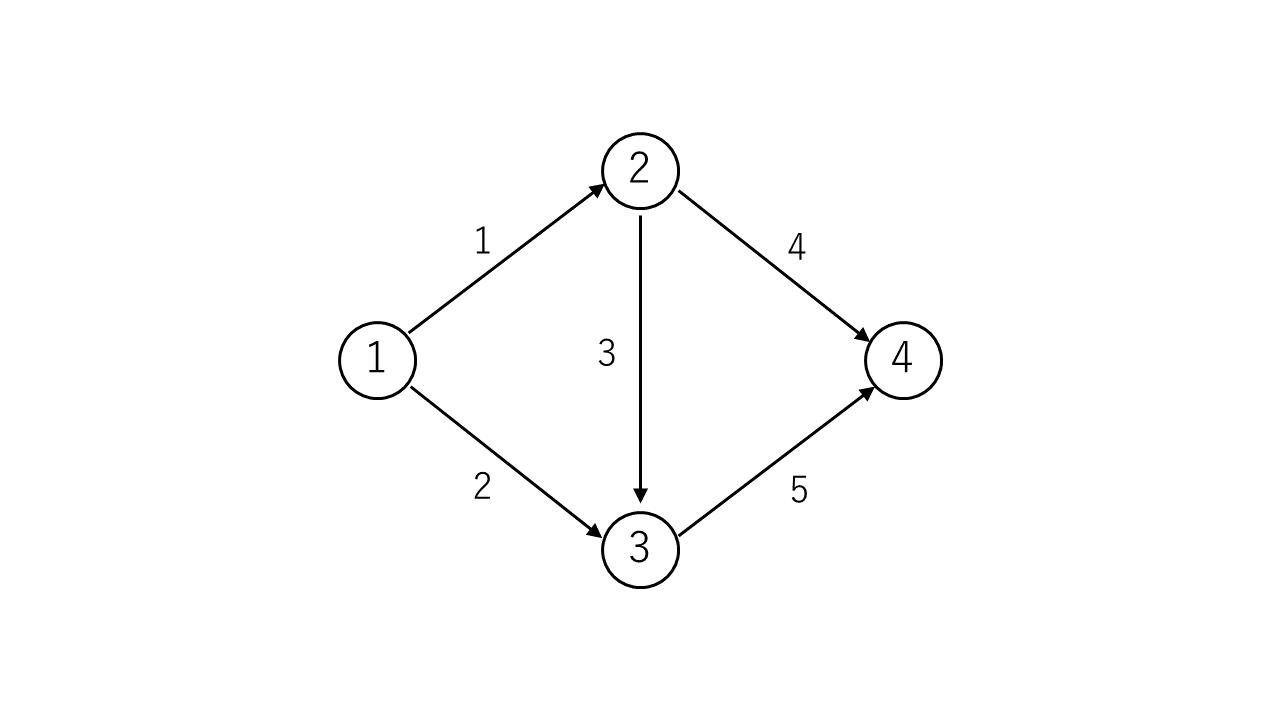
例えば長さ $2$ の辺素パス $(e_1, e_2) = (2, 5)$ を逆にすると、次の図のようにグラフ全体を強連結にすることができます。
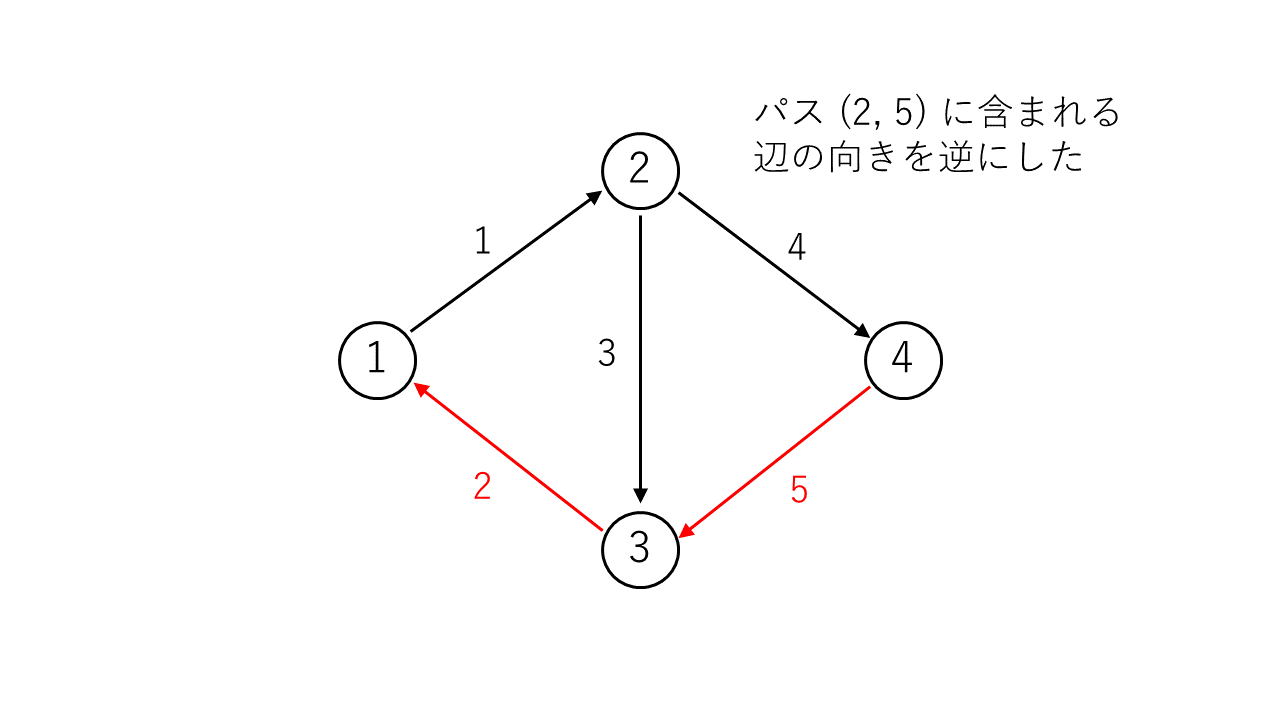
$1$ 本の辺を逆にしても強連結にはできないので、条件を満たすパスの長さの最小値は $2$ となります。
入力例 2
4 5
1 2
3 1
2 3
2 4
4 3
出力例 2
0
与えられるグラフは次のようになります。
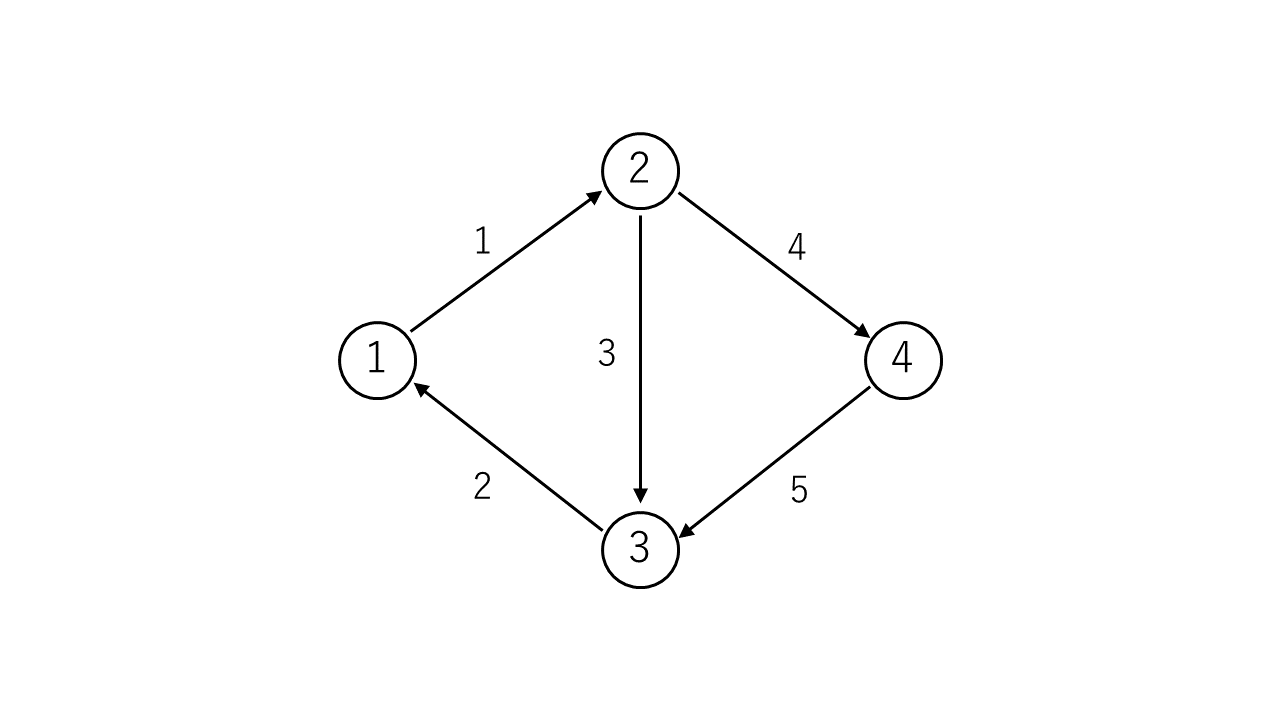
グラフはすでに強連結なので、辺を逆にする必要がありません。
入力例 3
2 1
1 2
出力例 3
-1
辺を逆にしてもしなくても、グラフは強連結になりません。