Icosahedron
問題
右手系の $3$ 次元直交座標 $(x,y,z)$ の上に、正二十面体があります。
正二十面体の展開図は以下のようになっており、各頂点にアルファベットまたは番号が振られています。ただし、図の手前側が組み立て後の正二十面体の外側になります。
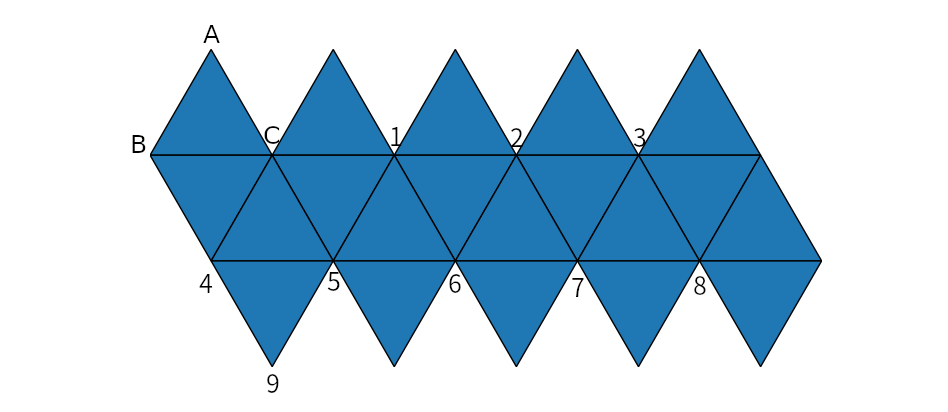
この正二十面体の $1$ つの面を構成する $3$ つの頂点 $A(A_x,A_y,A_z),B(B_x,B_y,B_z),C(C_x,C_y,C_z)$ の座標が与えられます。
その後、$N$ 個の整数 $v_1,v_2,\dots,v_N$ が与えられるので、各 $i$ ($1\leq i\leq N$) について頂点 $v_i$ の座標を出力してください。
制約
- $-200\leq A_x,A_y,A_z,B_x,B_y,B_z,C_x,C_y,C_z\leq 200$
- $1\leq N\leq 9$
- $1\leq v_i \leq 9$ ($1\leq i\leq N$)
- $v_i\neq v_j$ ($i \lt j$)
- 入力はすべて整数
- $A,B,C$ は正三角形をなす
入力
入力は以下の形式で標準入力から与えられます。
$A_x$ $A_y$ $A_z$ $B_x$ $B_y$ $B_z$ $C_x$ $C_y$ $C_z$ $N$ $v_1$ $v_2$ $\dots$ $v_N$
出力
$N$ 行出力してください。$i$ ($1\leq i\leq N$) 行目には頂点 $v_i$ の座標を出力してください。座標は $x$ 座標、$y$ 座標、$z$ 座標を順に空白区切りで整数または小数で出力してください。
各頂点の各成分について、想定解答との相対誤差または絶対誤差が $10^{-3}$ 以下のとき、正答とみなされます。
入力例 1
1 0 0 0 1 0 0 0 1 2 1 3
出力例 1
0.40127 -1.21676 0.40127 0.40127 0.40127 -1.21676