最適二分探索木

最適二分探索木とは、$n$ 個のキーと $n+1$ 個のダミーキーから、1回の探索にかかるコストの期待値が最小となるように構成された二分探索木のことです。

ソート済みの $n$ 個の異なるキーの列 $K = {k_1, k_2, ..., k_n} (k_1 < k_2 < ... < k_n)$ から、二分探索木を構成することを考えます。 各キー $k_i$ に対して探索が起きる確率は $p_i (1 \le i \le n)$ です。 また、探索は $K$ に含まれない値に対しても起こりうるので、$K$ に含まれない値を表す $n+1$ 個のダミーキー $d_0, d_1, d_2, ..., d_n$ を用意します。 具体的には、ダミーキー $d_i (0 \le i \le n)$ は以下のように定義されます。

• $i=0$ なら、$d_i$ は $k_1$ よりも小さいすべての値を表す。
• $i=n$ なら、$d_i$ は $k_n$ よりも大きいすべての値を表す。
• $1 \le i \le n-1$ なら、$d_i$ は $k_i$ よりも大きく、$k_{i+1}$ よりも小さいすべての値を表す。

各ダミーキー $d_i$ で探索が終わる確率は $q_i (0 \le i \le n)$ であることもわかっています。 ここで、$p_i (1 \le i \le n)$ と $q_i (0 \le i \le n)$ に関して、以下の等式が成立します。 \[ \sum_{i=1}^n p_i + \sum_{i=0}^n q_i = 1 \] これらの情報より、ある二分探索木 $T$ における1回の探索コストの期待値は以下の式で得られます。ここで、$depth_T(v)$ は $T$ における節点 $v$ の深さです。 \[ E_T = \sum_{i=1}^n (depth_T(k_i) + 1) \cdot p_i + \sum_{i=0}^n (depth_T(d_i) + 1) \cdot q_i \] この値を最小化するように構成された二分探索木を、最適二分探索木と呼びます。

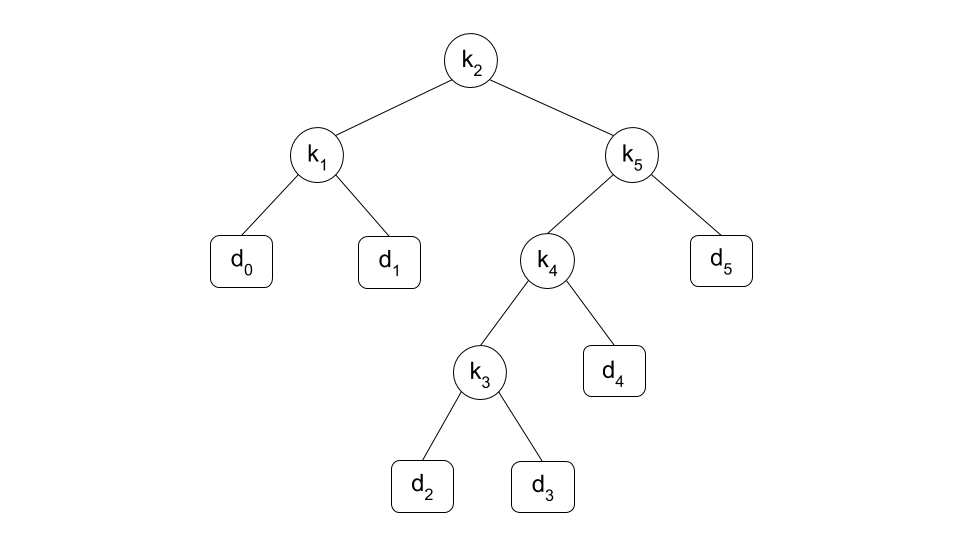
各キー$k_i$は内部節点、各ダミーキー$d_i$は葉になります。 例えば、入力例1の場合の最適二分探索木は以下のようになります。

課題

$n$ 個の各キーに対して探索が起きる確率 $p_i$ と、$n+1$ 個の各ダミーキーで探索が終わる確率 $q_i$ が与えられるので、このときの最適二分探索木の1回の探索コストの期待値を出力するプログラムを作成してください。

入力

$n$
$p_1$ $p_2$ ... $p_n$
$q_0$ $q_1$ $q_2$ ... $q_n$

1行目にキーの個数を表す整数 $n$ が与えられます。
2行目に各キーに対して探索が起きる確率 $p_i (1 \le i \le n)$ が小数点以下4桁の実数で与えられます。
3行目に各ダミーキーで探索が終わる確率 $q_i (0 \le i \le n)$ が小数点以下4桁の実数で与えられます。

出力

最適二分探索木の探索コストの期待値を1行に出力してください。絶対誤差が $10^{-4}$ 以下のとき正答と判定されます。

制約

• $1 \le n \le 500$
• $0 \lt p_i, q_i \lt 1$
• $\displaystyle \sum_{i=1}^n p_i + \sum_{i=0}^n q_i = 1$

入力例 1

5
0.1500 0.1000 0.0500 0.1000 0.2000
0.0500 0.1000 0.0500 0.0500 0.0500 0.1000

出力例 1

2.75000000

入力例 2

7
0.0400 0.0600 0.0800 0.0200 0.1000 0.1200 0.1400
0.0600 0.0600 0.0600 0.0600 0.0500 0.0500 0.0500 0.0500

出力例 2

3.12000000

---