Depth First Search

Depth-first search (DFS) follows the strategy to search ”deeper” in the graph whenever possible. In DFS, edges are recursively explored out of the most recently discovered vertex $v$ that still has unexplored edges leaving it. When all of $v$'s edges have been explored, the search ”backtracks” to explore edges leaving the vertex from which $v$ was discovered.

This process continues until all the vertices that are reachable from the original source vertex have been discovered. If any undiscovered vertices remain, then one of them is selected as a new source and the search is repeated from that source.

DFS timestamps each vertex as follows:

• $d[v]$ records when $v$ is first discovered.
• $f[v]$ records when the search finishes examining $v$’s adjacency list.

Write a program which reads a directed graph $G = (V, E)$ and demonstrates DFS on the graph based on the following rules:

• $G$ is given in an adjacency-list. Vertices are identified by IDs $1, 2,... n$ respectively.
• IDs in the adjacency list are arranged in ascending order.
• The program should report the discover time and the finish time for each vertex.
• When there are several candidates to visit during DFS, the algorithm should select the vertex with the smallest ID.
• The timestamp starts with 1.

Input

In the first line, an integer $n$ denoting the number of vertices of $G$ is given. In the next $n$ lines, adjacency lists of $u$ are given in the following format:

$u$ $k$ $v_1$ $v_2$ ... $v_k$

$u$ is ID of the vertex and $k$ denotes its degree. $v_i$ are IDs of vertices adjacent to $u$.

Output

For each vertex, print $id$, $d$ and $f$ separated by a space character in a line. $id$ is ID of the vertex, $d$ and $f$ is the discover time and the finish time respectively. Print in order of vertex IDs.

Constraints

• $1 \leq n \leq 100$

Sample Input 1

4
1 1 2
2 1 4
3 0
4 1 3

Sample Output 1

1 1 8
2 2 7
3 4 5
4 3 6

Sample Input 2

6
1 2 2 3
2 2 3 4
3 1 5
4 1 6
5 1 6
6 0

Sample Output 2

1 1 12
2 2 11
3 3 8
4 9 10
5 4 7
6 5 6

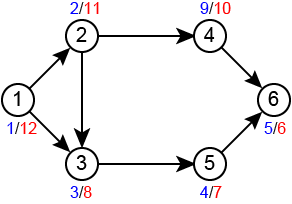
This is example for Sample Input 2 (discover/finish)

Reference

Introduction to Algorithms, Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. The MIT Press.

---