ハフマン符号

与えられた文字列に出現する各文字の種類ごとに、異なるビット文字列の符号語を割り当て、文字列をビット文字列へ符号化します。この時、どの符号語も別の符号語の接頭語とならないように符号語を割り当てると、得られたビット文字列符号から一意に元の文字列を定めることができます。

このような符号語の割り当てを求める方法の一つに、ハフマンの符号化アルゴリズムがあります。このアルゴリズムは、任意の文字列に対して最短の自然数長ビット文字列符号を生成します。

たとえば、文字列に出現する文字の種類が'a', 'b', 'c', 'd', 'e', 'f'で、その出現頻度が45, 13, 12, 16, 9, 5の文字列を考えます。この文字列に対してハフマンの符号化アルゴリズムを適用すると、以下の表に示す符号語を得ることができ、これが最適な符号語の割り当てとなります。

	a	b	c	d	e	f
出現頻度	45	13	12	16	9	5
符号語	0	101	100	111	1101	1100

ハフマンの符号化アルゴリズムは、以下の図のようなハフマン木と呼ばれる全二分木を構成します。

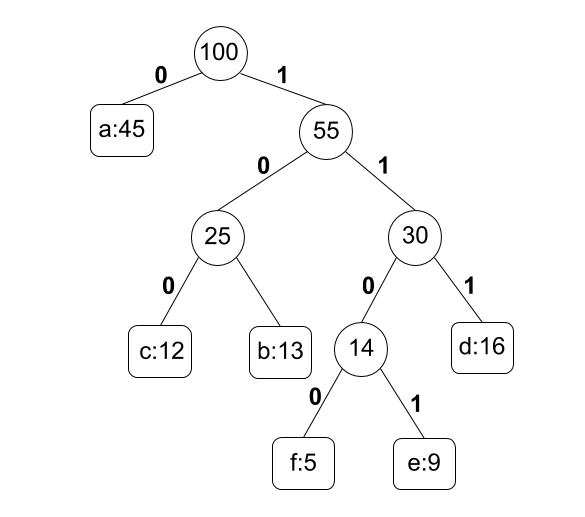
まず、それぞれの文字の種類ごとに、文字の種類とその出現頻度を持つ節点を作ります。これらの節点は親を持ちません。その後、以下の手順を繰り返しハフマン木を生成します。

1. 親を持たない節点のうち、最も出現頻度の低い2つの節点$x, y$を選ぶ
2. $x$と$y$の出現頻度の和を出現頻度とする新たな節点 $z$ を作る
3. $z$を$x$と$y$の親にする
4. 親を持たない節点が1つなら終了.そうでないなら 1. へ戻る

ハフマン木の葉を除く各節点の左の子への辺と右の子への辺のそれぞれに0と1を割り当てます。根から葉へ向かうパス上の辺に割り当てられた0または1を順番に連結することで、その葉に対応する文字の符号語が得られます。

課題

文字列$S$が入力として与えられます。ハフマンの符号化アルゴリズムを用いて$S$の各文字に符号語を割り当てたときに、$S$を符号化して得られるビット文字列の長さを出力するプログラムを作成してください。

入力

$S$

文字列$S$が1行に与えられます。

出力

ビット文字列の長さを1行に出力してください。

制約

• $1 \le |S| \le 10^5$
• $S$ は英小文字からなる

入力例 1

abca

出力例 1

6

例えば上記のアルゴリズムを利用して、aに0、bに10、cに11を符号語として割り当てると、得られるビット列は010110となり、6が答えになります。

入力例 2

aaabbcccdeeeffg

出力例 2

41

入力例 3

z

出力例 3

1

---