Exhaustive Search

Write a program which reads a sequence A of n elements and an integer M, and outputs "yes" if you can make M by adding elements in A, otherwise "no". You can use an element only once.

You are given the sequence A and q questions where each question contains M_i.

Input

In the first line n is given. In the second line, n integers are given. In the third line q is given. Then, in the fourth line, q integers (M_i) are given.

Output

For each question M_i, print yes or no.

Constraints

• n ≤ 20
• q ≤ 200
• 1 ≤ elements in A ≤ 2000
• 1 ≤ M_i ≤ 2000

Sample Input 1

5
1 5 7 10 21
8
2 4 17 8 22 21 100 35

Sample Output 1

no
no
yes
yes
yes
yes
no
no

Notes

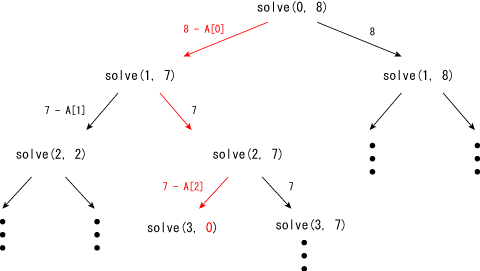
You can solve this problem by a Burte Force approach. Suppose solve(p, t) is a function which checkes whether you can make t by selecting elements after p-th element (inclusive). Then you can recursively call the following functions:

solve(0, M)
solve(1, M-{sum created from elements before 1st element})
solve(2, M-{sum created from elements before 2nd element})
...

The recursive function has two choices: you selected p-th element and not. So, you can check solve(p+1, t-A[p]) and solve(p+1, t) in solve(p, t) to check the all combinations.

For example, the following figure shows that 8 can be made by A[0] + A[2].

---