二分探索木I
探索木は、挿入、検索、削除などの操作が行えるデータ構造で、辞書あるいは優先度付きキューとして用いることができます。探索木の中でも最も基本的なものが二分探索木です。二分探索木は、各節点にキーを持ち、次に示す二分探索木条件(Binary search tree property) を常に満たすように構築されます:
- $x$ を2分探索木に属するある節点とする。 $y$ を $x$ の左部分木に属する節点とすると、$y$ のキー $\leq x$のキーである。また、$y$ を $x$ の右部分木に属する節点とすると、$x$ のキー $\leq y$ のキーである。
次の図は二分探索木の例です。
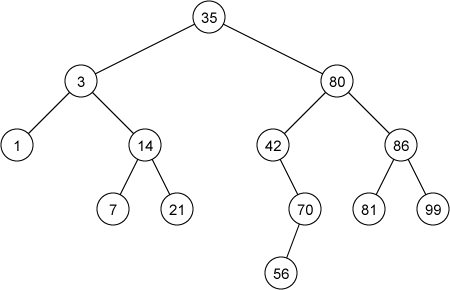
例えば、キーが80の節点の左部分木に属する節点のキーは80以下であり、右部分木に属する節点のキーは80以上になっています。二分探索木に中間順巡回を行うと、昇順に並べられたキーの列を得ることができます。
二分探索木は、データの挿入や削除が行われても常にこのような条件が全ての節点で成り立つように実装しなければなりません。リストと同様に、節点をポインタで連結することで木を表し、各節点には値(キー)に加えその親、左の子、右の子へのポインタを持たせます。
二分探索木 $T$ に新たに値 $v$ を挿入するには以下の疑似コードに示す insert を実行します。insert は、キーが $v$、左の子が $NIL$、右の子が $NIL$ であるよな節点 $z$ を受け取り、$T$ の正しい位置に挿入します。
1 insert(T, z) 2 y = NIL // x の親 3 x = 'T の根' 4 while x ≠ NIL 5 y = x // 親を設定 6 if z.key < x.key 7 x = x.left // 左の子へ移動 8 else 9 x = x.right // 右の子へ移動 10 z.p = y 11 12 if y == NIL // T が空の場合 13 'T の根' = z 14 else if z.key < y.key 15 y.left = z // z を y の左の子にする 16 else 17 y.right = z // z を y の右の子にする
二分探索木 $T$ に対し、以下の命令を実行するプログラムを作成してください。
- insert $k$: $T$にキー $k$ を挿入する。
- print: キーを木の中間順巡回(inorder tree walk)と先行順巡回(preorder tree walk)アルゴリズムで出力する。
挿入のアルゴリズムは上記疑似コードに従ってください。
入力
入力の最初の行に、命令の数 $m$ が与えられます。続く $m$ 行目に、insert $k$ または print の形式で命令が1行に与えられます。
出力
print命令ごとに、中間順巡回アルゴリズム、先行順巡回アルゴリズムによって得られるキーの順列をそれぞれ1行に出力してください。各キーの前に1つの空白を出力してください。
制約
- 命令の数は $500,000$ を超えない。
- print 命令の数は $10$ を超えない。
- $-2,000,000,000 \leq キー \leq 2,000,000,000$
- 上記の疑似コードのアルゴリズムに従う場合、木の高さは 100 を超えない。
- 二分探索木中のキーに重複は発生しない。
入力例 1
8 insert 30 insert 88 insert 12 insert 1 insert 20 insert 17 insert 25 print
出力例 1
1 12 17 20 25 30 88 30 12 1 20 17 25 88
参考文献
Introduction to Algorithms, Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. The MIT Press.