Treap
二分探索木は、挿入されるデータ列の特徴によっては、偏った木になり、検索・挿入・削除操作の効率が悪くなります。例えば、整列された$n$個のデータが順番に挿入されれば、木はリストのような形になり、その高さは$n$になります。挿入されるデータが固定されていれば、要素をランダムにシャッフルすることにより平衡な木を構築することができるでしょう。しかし、データ構造としての二分木では要求に応じて異なる操作が繰り返し行われるため、適宜データを一つずつ処理しながら、常に平衡な状態を保つ必要があります。
二分木の各節点に、ランダムに選択された優先度を割り当て、以下の条件を満たすように節点を順序付けることによって、平衡な二分木を保つことができます。ここで、各節点のキー(key)と優先度(priority)はそれぞれ重複がないものとします。
- 二分探索木条件. $v$が$u$の左の子なら$v.key < u.key$ かつ $v$が$u$の右の子なら $u.key < v.key$
- ヒープ条件.$v$が$u$の子なら$v.priority < u.priority$
このような木を、二分探索木とヒープの特徴からTreap ( tree + heap ) と呼びます。
例えば、次の図はTreapの例です。
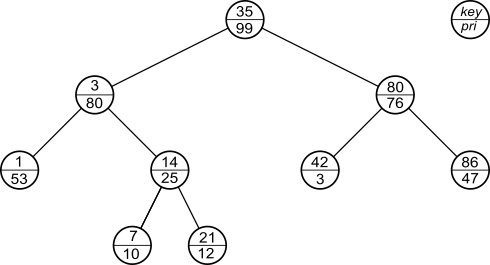
挿入
Treapに新たにデータを挿入するには、キーに加えランダムに選択した優先度を割り当てた節点を、まずは通常の二分探索木と同様の方法で挿入します。例えば、上のTreapにkey = 6, priority = 90 である節点を挿入すると次のようになります。
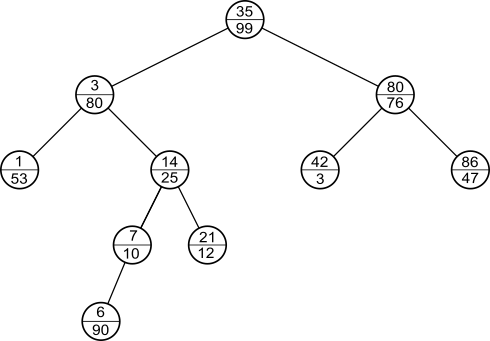
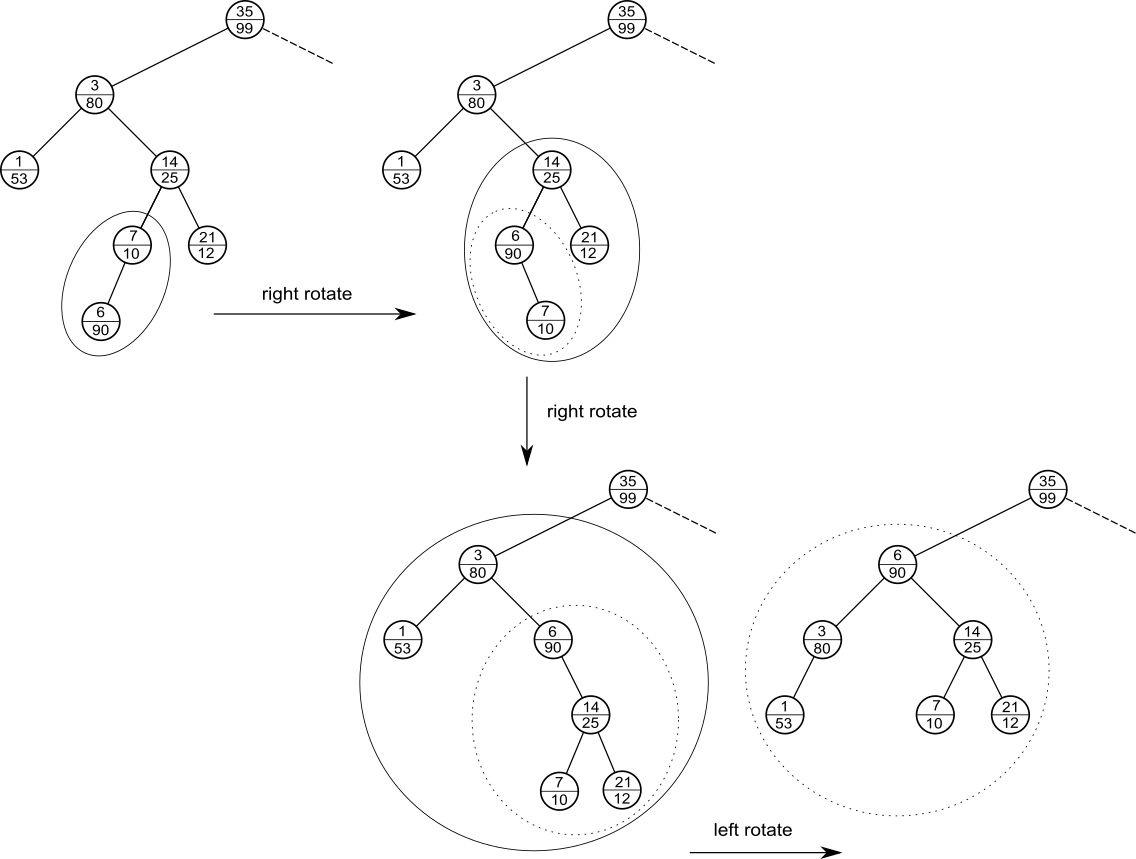
このままの状態では、ヒープ条件を破ってしまうため、ヒープ条件を満たすまで回転を繰り返します。回転とは、次の図のように、二分探索木条件を満たしつつ、親子関係を逆転させる操作です。

回転は次のプログラムのようにポインタを繋ぎ変えます。
rightRotate(Node t)
Node s = t.left
t.left = s.right
s.right = t
return s // root of the subtree
|
leftRotate(Node t)
Node s = t.right
t.right = s.left
s.left = t
return s // root of the subtree
|
上のTreapに回転操作を行うと以下のように二分探索木が構築されます。
条件を満たすようにTreapに新しい要素を挿入するinsert操作は以下のようになります。
insert(Node t, int key, int priority) // 再帰的に探索
if t == NIL
return Node(key, priority) // 葉に到達したら新しい節点を生成して返す
if key == t.key
return t // 重複したkeyは無視
if key < t.key // 左の子へ移動
t.left = insert(t.left, key, priority) // 左の子へのポインタを更新
if t.priority < t.left.priority // 左の子の方が優先度が高い場合右回転
t = rightRotate(t)
else // 右の子へ移動
t.right = insert(t.right, key, priority) // 右の子へのポインタを更新
if t.priority < t.right.priority // 右の子の方が優先度が高い場合左回転
t = leftRotate(t)
return t
削除
Treapの節点を削除する場合は、以下の手順で対象となる節点を回転によって葉まで移動した後、削除します。
delete(Node t, int key)
if t == NIL
return NIL
if key < t.key // 削除対象を検索
t.left = delete(t.left, key)
else if key > t.key
t.right = delete(t.right, key)
else
return _delete(t, key)
return t
_delete(Node t, key) // 削除対象の節点の場合
if t.left == NIL && t.right == NIL // 葉の場合
return NIL
else if t.left == NIL // 右の子のみを持つ場合左回転
t = leftRotate(t)
else if t.right == NIL // 左の子のみを持つ場合右回転
t = rightRotate(t)
else // 左の子と右の子を両方持つ場合
if t.left.priority > t.right.priority // 優先度が高い方を持ち上げる
t = rightRotate(t)
else
t = leftRotate(t)
return delete(t, key)
Treap $T$ に対して、以下の命令を、上記のアルゴリズムに基づいて実行するプログラムを作成してください。
- insert ($k$, $p$): $T$ にキーが $k$、優先度が$p$の要素 を挿入する。
- find ($k$): $T$ にキー $k$ が存在するか否かを報告する。
- delete ($k$): キー $k$ を持つ節点を削除する。
- print(): キーを木の中間順巡回(inorder tree walk)と先行順巡回(preorder tree walk)アルゴリズムで出力する。
入力
入力の最初の行に、命令の数 $m$ が与えられます。続く$m$ 行に、insert $k \; p$、find $k$、delete $k$ または print の形式で命令が1行に与えられます。
出力
find $k$ 命令ごとに、$T$ に $k$ が含まれる場合 yes と、含まれない場合 no と1行に出力してください。
さらに print 命令ごとに、中間順巡回アルゴリズム、先行順巡回アルゴリズムによって得られるキーの順列をそれぞれ1行に出力してください。各キーの前に1つの空白を出力してください。
制約
- 命令の数は$200,000$を超えない。
- $0 \leq k, p \leq 2,000,000,000$
- 上記のアルゴリズムに従う場合、木の高さは $50$ を超えない。
- 二分探索木中のキーに重複は発生しない。
- 二分探索木中の優先度に重複は発生しない。
- print命令の数は$10$を超えない。
- 出力のサイズは$10$ Mバイトを超えない。
入力例 1
16 insert 35 99 insert 3 80 insert 1 53 insert 14 25 insert 80 76 insert 42 3 insert 86 47 insert 21 12 insert 7 10 insert 6 90 print find 21 find 22 delete 35 delete 99 print
出力例 1
1 3 6 7 14 21 35 42 80 86 35 6 3 1 14 7 21 80 42 86 yes no 1 3 6 7 14 21 42 80 86 6 3 1 80 14 7 21 42 86
参考文献
- Introduction to Algorithms, Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. The MIT\ Press.
- Randomized Search Trees, R. Seidel, C.R. Aragon.