最大ヒープ
「節点のキーがその親のキー以下である」という max-ヒープ条件を満たすヒープを、max-ヒープと呼びます。max-ヒープでは、最大の要素が根に格納され、ある節点を根とする部分木の節点のキーは、その部分木の根のキー以下となります。親子間のみに大小関係があり、兄弟間に制約はないことに注意してください。
例えば、下図はmax-ヒープの例です。
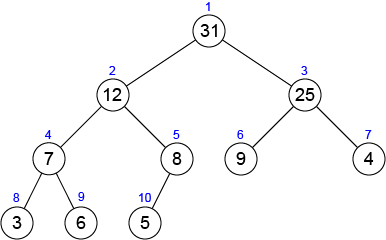
与えられた配列から以下の疑似コードに従ってmax-ヒープを構築するプログラムを作成してください。
$maxHeapify(A, i)$ は、節点 $i$ を根とする部分木が max-ヒープになるよう $A[i]$ の値を max-ヒープの葉へ向かって下降させます。ここで $H$ をヒープサイズとします。
1 maxHeapify(A, i) 2 l = left(i) 3 r = right(i) 4 // 左の子、自分、右の子で値が最大のノードを選ぶ 5 if l ≤ H and A[l] > A[i] 6 largest = l 7 else 8 largest = i 9 if r ≤ H and A[r] > A[largest] 10 largest = r 11 12 if largest ≠ i // i の子の方が値が大きい場合 13 A[i] と A[largest] を交換 14 maxHeapify(A, largest) // 再帰的に呼び出し
次の buildMaxHeap(A) はボトムアップに maxHeapify を適用することで配列 $A$ を max-ヒープに変換します。
1 buildMaxHeap(A) 2 for i = H/2 downto 1 3 maxHeapify(A, i)
入力
入力の最初の行に、ヒープのサイズ $H$ が与えられます。続いて、ヒープの節点の値を表す $H$ 個の整数が節点の番号が 1 から $H$ に向かって順番に空白区切りで与えられます。
出力
max-ヒープの節点の値を節点の番号が 1 から $H$ に向かって順番に1行に出力してください。各値の直前に1つの空白文字を出力してください。
制約
- $1 \leq H \leq 500,000$
- $-2,000,000,000 \leq 節点の値 \leq 2,000,000,000$
入力例 1
10 4 1 3 2 16 9 10 14 8 7
出力例 1
16 14 10 8 7 9 3 2 4 1
参考文献
Introduction to Algorithms, Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. The MIT Press.