Tetrahedron

Aizu painters apply color to walls in a unique way. The wall is sectioned in a triangular coordinate system as shown in the following figure.

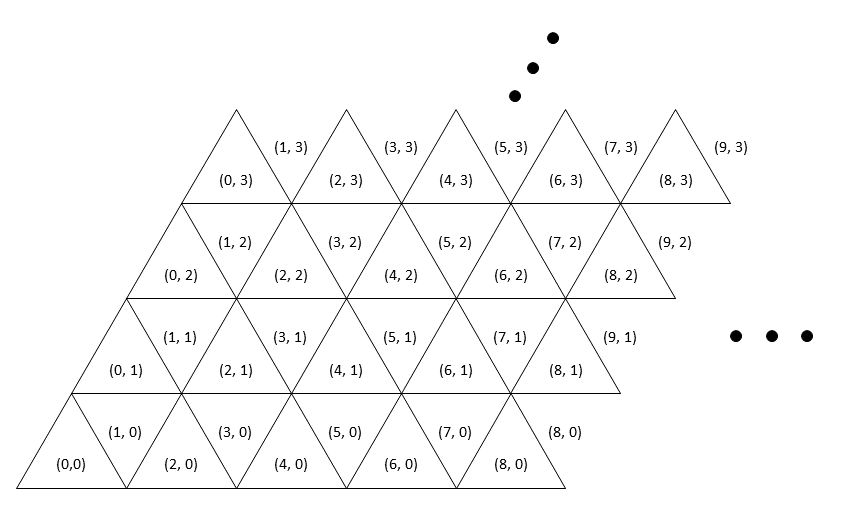
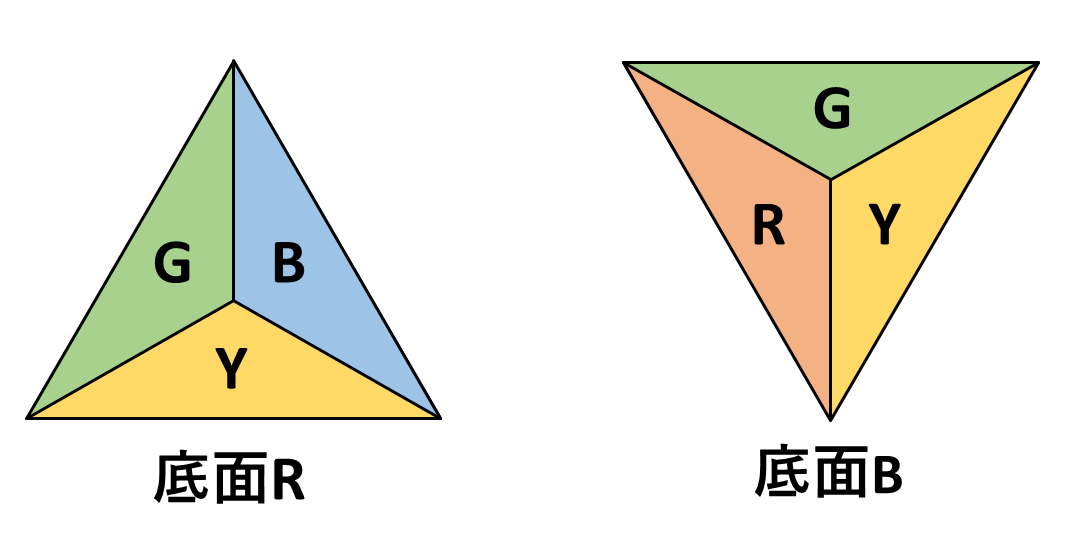
There is a tetrahedron that is sufficiently soaked with paint on its surfaces. They roll this tetrahedron instead of a roller. Each surface of the tetrahedron is impregnated with paint of the four colors R, G, B, and Y, as shown in the following figure, so that the compartments whose surfaces touch can be painted.

The painter starts with the compartment (0,0) and paints the wall by rolling it around one side of the tetrahedron as an axis. The tetrahedron is not moved away from the wall or slid over the wall until the work is finished. For example, if you roll the tetrahedron appropriately, you will get a pattern on the wall as shown in the following figure.

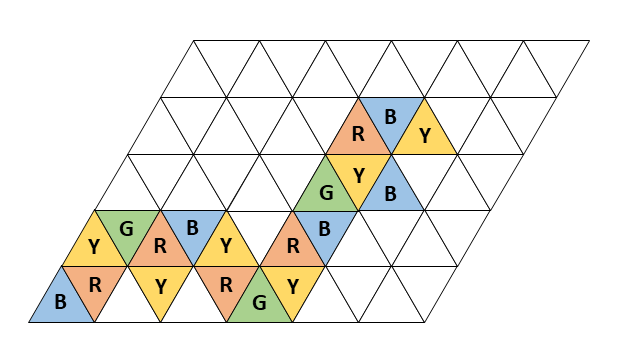
If you paint in this way, once you have decided on the colors of the first (0,0) and second (1,0) compartments to pass through, all the compartments will have the same color, no matter how you roll them afterwards.

Given the colors of the first and second compartments to pass through, and also given one or more compartments for which you want to find the color, write a program to find the color of each specified compartment.

Input

The input is given in the following form.

$c_1$ $c_2$
$N$
$x_1$ $y_1$
$x_2$ $y_2$
:
$x_N$ $y_N$

In the first line, the colors $c_1$ and $c_2$ ('R', 'G', 'B', or 'Y ') are given. The second line gives the number of plots, $N$ ($1 \leq N \leq 100$), for which the color is to be determined. In the following $N$ lines, the coordinates $x_i$, $y_i$ ($0 \leq x_i,y_i \leq 100$) of the plot for which we want to find the color are given.

Output

The output consists of $N$ lines. Output a single character representing the color of the $i$-th parcel for which we want to find the color on the $i$-th line.

Sample Input and Output

Sample Input

B R
2
8 3
1 1	

Sample Output

Y
G

---