F : Tree / 木
問題文
大きさ N の根付き木がある。 各頂点には 0 から N−1 までの番号が付けられ、根が 0である。 任意の辺の両端の頂点について、割り当てられた整数は根に近いほうが小さい。初めは全ての辺の重みは 0 である。
この木に対する Q 個のクエリを順に処理せよ。クエリには以下の 2 種類がある。
- 頂点 u, v の距離(パスに含まれる辺の重みの和)を求める。
- 頂点 v の子孫(自身を含まない)に接続する辺の重みを全て x 増加させる。
入力
入力は以下の形式からなる。
N Q
a_0 b_0
…
a_{N−2} b_{N−2}
q_0
…
q_{Q−1}
a_i,b_i は i 番目の辺が結ぶ頂点である。 q_i は i 番目のクエリを表す 3 つの整数であり、次のうちいずれかである。
- 0 \ u_i \ v_i : 頂点 u_i, v_i の距離を求める。
- 1 \ v_i \ x_i : 頂点 v_i の子孫に接続する辺の重みを全て x_i 増加させる。
制約
- 入力はすべて整数である
- 2 \≤ N \≤ 150\,000
- 1 \≤ Q \≤ 150\,000
- 0 \≤ a_{i},b_{i},u_{i},v_{i} \≤ N−1
- a_{i} < b_{i}
- 0 \≤ x_{i} \≤ 300
出力
距離を求めるクエリのたびに、結果を1行で出力せよ。
注意
この問題では入出力が非常に大きくなりうるので高速な関数を使用してほしい。
サンプル
サンプル入力1
9 6 0 1 0 2 0 3 1 4 1 5 4 6 5 7 5 8 1 0 1 1 1 2 0 6 3 1 5 5 1 8 4 0 4 3
サンプル出力1
8 5
図のようになる。
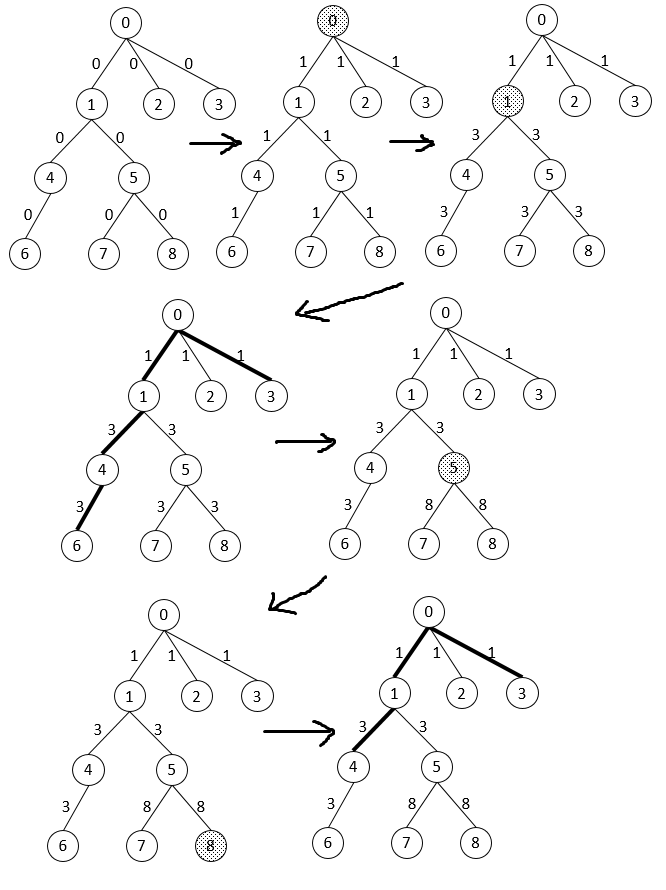
サンプル入力2
13 7 0 1 1 2 2 3 1 4 3 5 1 6 2 7 0 8 7 9 5 10 8 11 1 12 1 2 143 0 8 7 0 10 6 1 1 42 1 6 37 0 3 6 1 6 38
サンプル出力2
143 429 269